[ad#ad5]
◆問題:乳がん検査が陽性だと乳がんの確率は?
最近、『賢く決めるリスク思考』という非常に面白い本を読みました。世の中の確実性・リスク・不確実性について正しい知識をもって対処することが必要ということを説いている本ですが、興味ある方はぜひ読んでみてください。
さて、この本のなかで以下のような問題がでてきます。ぜひ、医療従事者であるなら解いてみてください(以下、書籍より一部参照)。
【女性の問いに答えるために必要な情報】
・女性が乳がんにかかっている確率(有病率)は1%。
・女性が乳がんにかかっている場合、検査で陽性と判定される確率(感度)は90%。
・女性が乳がんにかかっていないにもかかわらず陽性と判定される確率(偽陽性率)は9%。
【選択肢】
①10人につき9人(90%)
②10人につき8人(80%)
③10人につき1人(10%)
④100人につき1人(1%)
◆じつは医師でもよくわかってない統計の読み方
本のなかではこの問題を婦人科医160人に答えてもらっています。以下がそのグラフです。
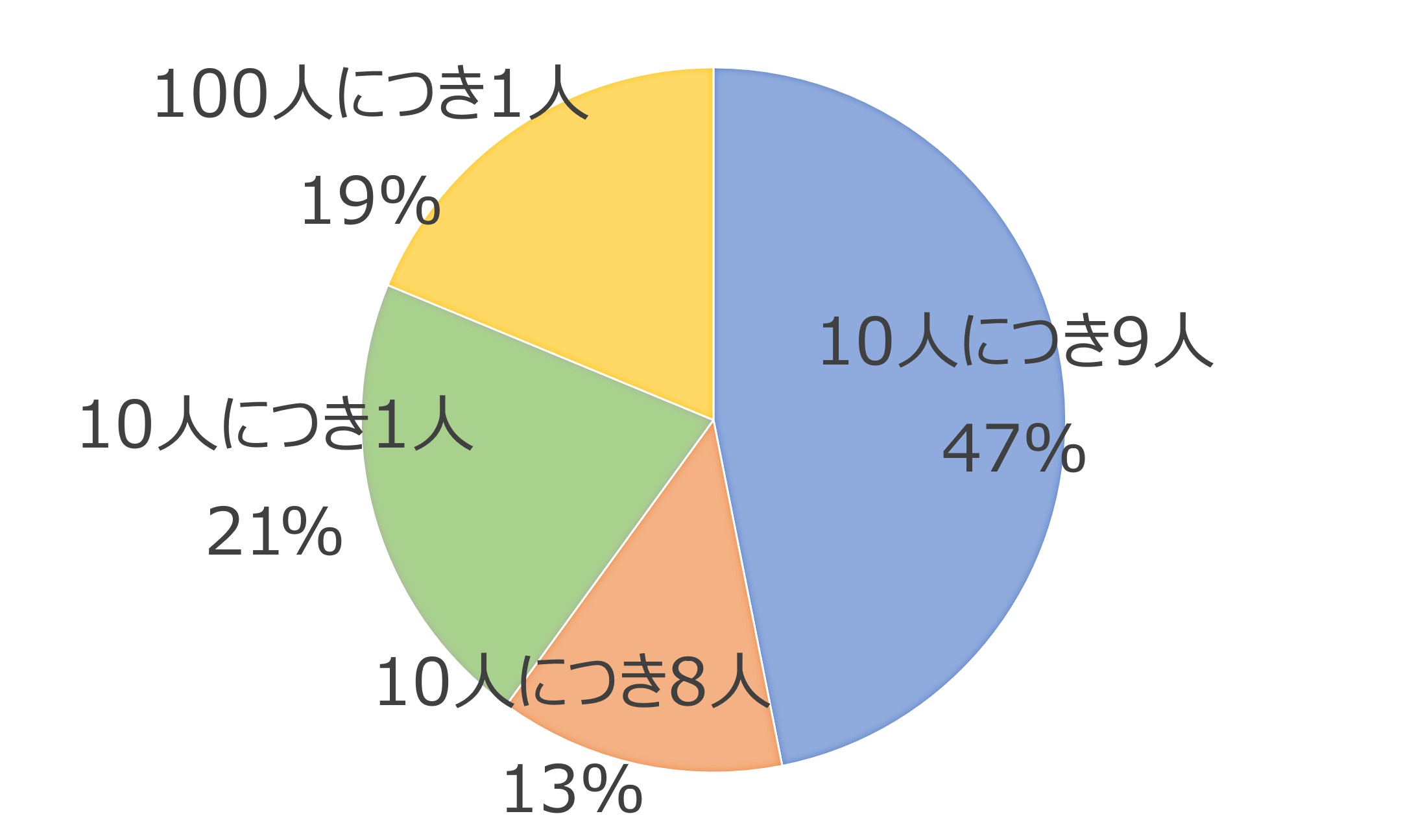
婦人科医の答えは分散しています。つまり、統計分析の知識があまりないということが示唆されますね。この婦人科医たちは患者が本当に乳がんであるかどうかの確率を正確に伝えることができないのです。
医師の統計的知識の不足は以下のように報告されています。
・標準的な統計の入門講義をひとつしか受けていない医師の知識は、『New England Journal of Medicine』に掲載されている論文のうちの約5分の1しか理解できない(1)。
・医療分野で使われている統計手法に関するテストに対する医学研修生の正答率は平均して50%以下、研究に関する訓練を受けている医学校の教授陣でも75%に届かなかった(2)。
これらはアメリカの報告ですが、日本の医師が突出して統計手法に秀でているとは考えにくいので、統計手法に関する知識はアメリカと同程度かそれ以下であると推測されます。
さて、話を戻します。さきほどの乳がんの問題の答えは「③10人につき1人」です。そして、本のなかでは『自然頻度』という思考法を導入することで、さきほどの160人の婦人科医の正答率は87%までに向上しました(導入前は21%)。
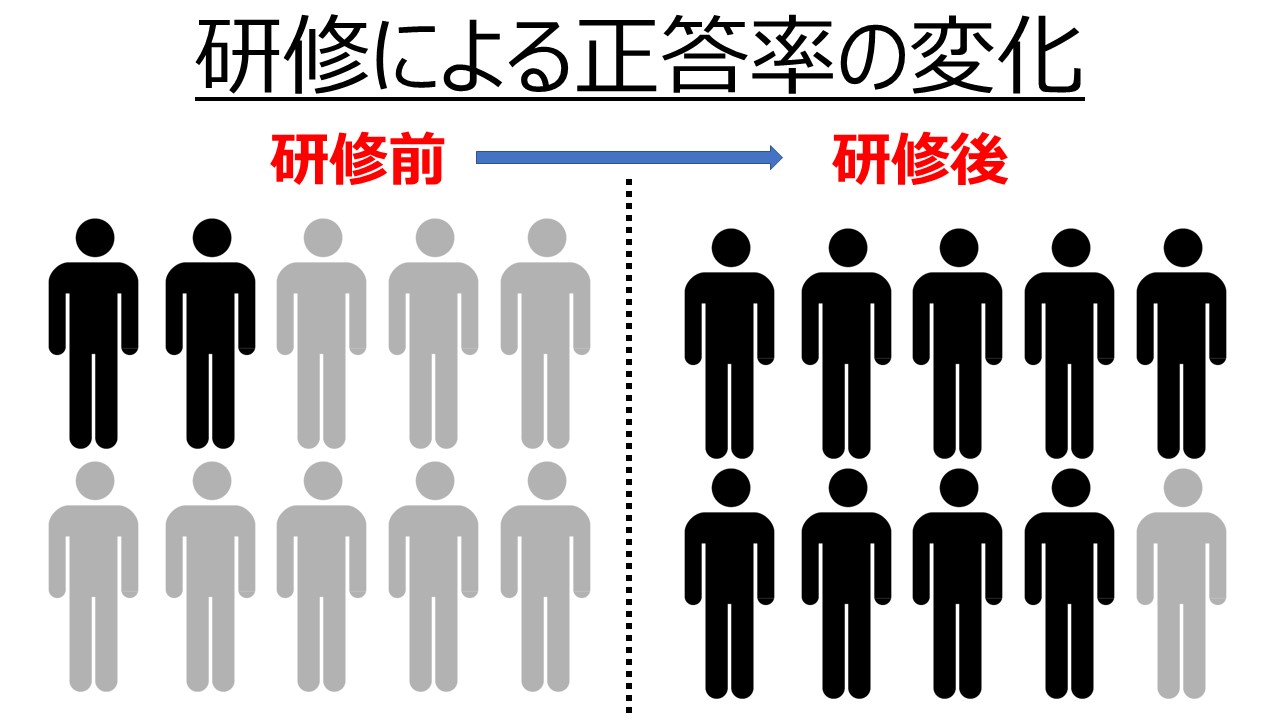
その方法がリハビリテーション(理学療法士)でも使えると思いましたので、まとめていきたいとおもいます。まずは乳がんの問題を自然頻度で解いてみましょう。
◆確率ではなく自然頻度で考える
さきほどの乳がんの問題を「確率」で考えると以下のようになります。
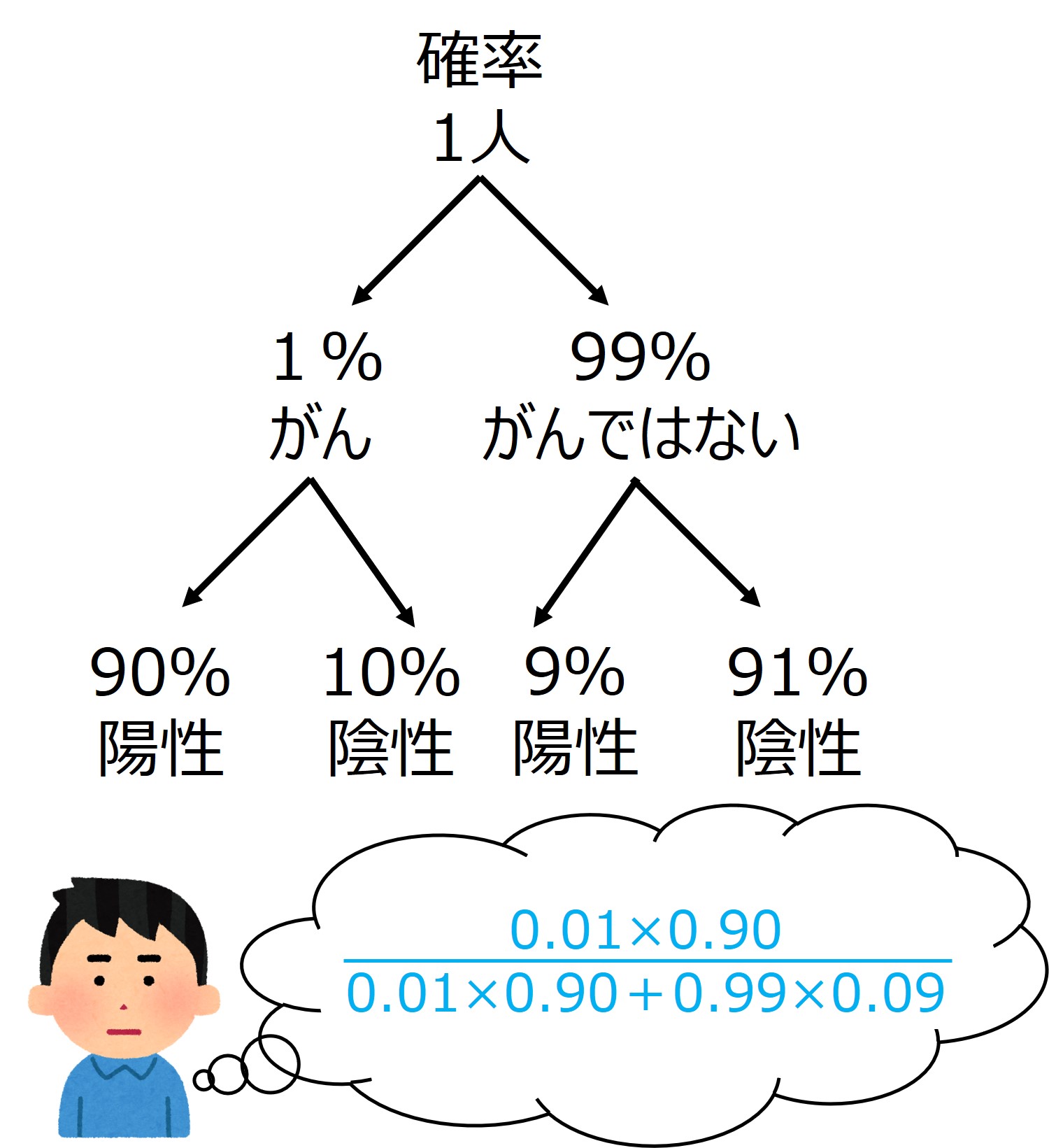
資料(3)参照作成
教科書や論文などでは上図のように書かれていることが多いと思います。相対リスク○○%低下とか有病率は○○%といった感じですね。
たいして、「自然頻度」では以下のような思考過程になります。
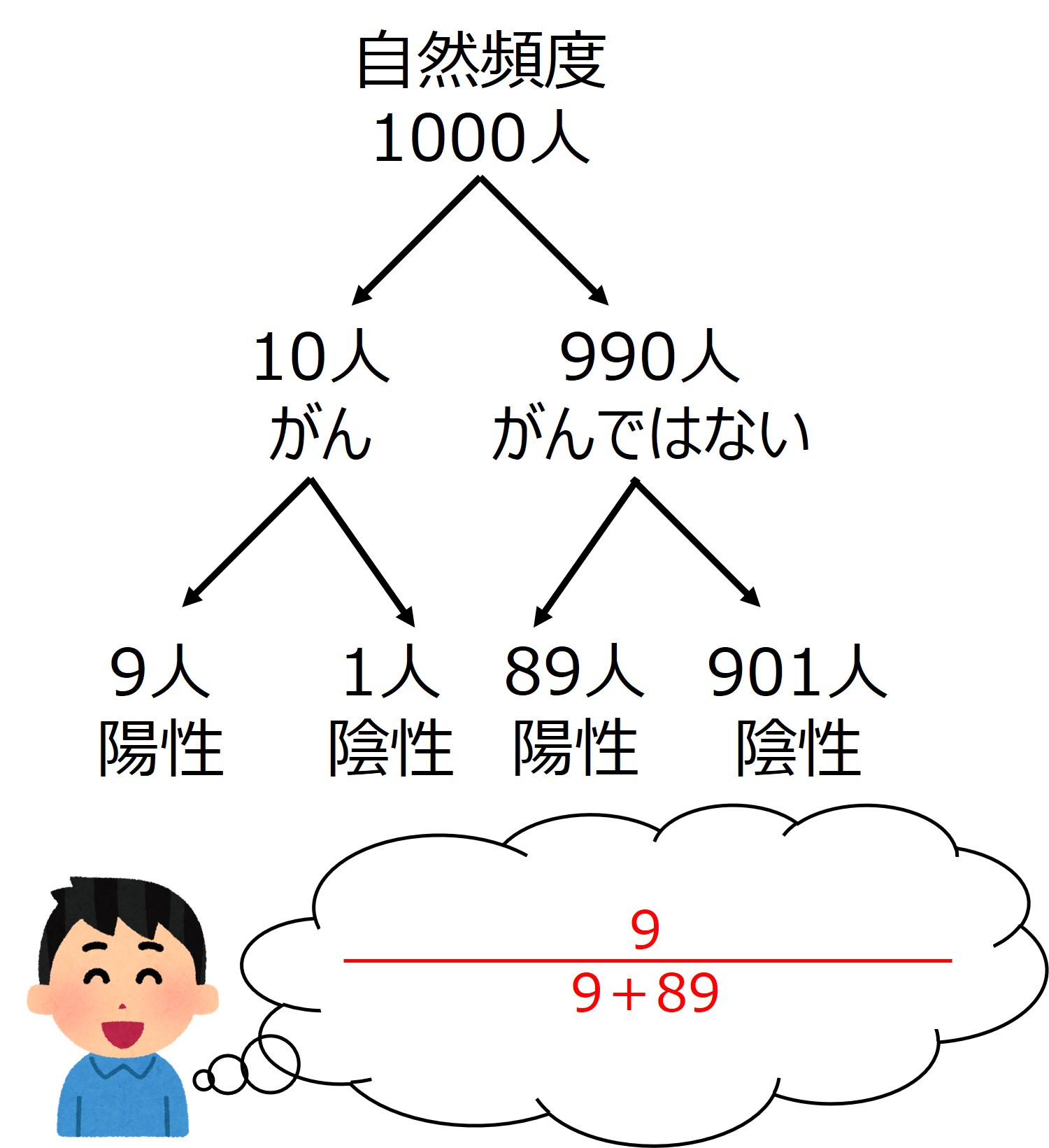
資料(3)参照作成
だいぶ理解しやすくなったのではないでしょうか?ではさきほどの問題を振りかえってみます。さきほどの問題は「乳がんの検査で陽性になった患者さんが実際にがんである確率は?」というものでした。
確率で考えるとよほど計算に得意でないと解けませんが、自然頻度で考えると暗算でもいけますね。「がんで陽性になった人+がんではないけど陽性になった人の総和」と「がんで陽性になった人」の比率を見ればいいわけです。
・9/9+89=9/98(≒約9%)
つまり、1000人のうち約98人(9人+89人)が検査で陽性と判定されます。そのうち実際にがんにかかっているのは9人(約9%)。検査で10人が陽性判定を受けたとすると、そのうち実際に乳がんであるのはおおよそ1人ということですね。こういった「検査が陽性のときに病気の確率がどれくらいか?」というのを「陽性的中率」といいます。
確率と自然頻度の思考過程は比較は以下のようになります。

◆ヘルニアの検査で陽性の場合を考えてみる
では、乳がんではなく整形疾患分野で考えてみます。
【男性の問いに答えるために必要な情報】
・男性がヘルニアにかかっている確率(有病率)は1%。
・SLR検査:感度80%、特異度90%。
※情報は便宜上わかりやすい数値にしており正確ではありません。
ヘルニアの有病率が1%だとすると、1000人のうち10人はヘルニア、990人はヘルニアではないということになります。
感度が80%ですので10人のうち8人はSLR検査で陽性(10×0.8)、2人は偽陰性(ヘルニアなのに検査が陰性)になります。また特異度が90%なのでヘルニアでない人では891人は陰性(990×0.9)、残りの99人はSLR検査が偽陽性(ヘルニアではないけど検査が陽性)となります。
さて、「ヘルニアで陽性になった人+ヘルニアでないけど陽性になった人の総和」と「ヘルニアで陽性になった人」の比率を見てみます。
・8/8+99=8/107(≒約7.5%)
つまり、1000人のうち約107人(8人+99人)が検査で陽性と判定されます。そのうち実際にヘルニアにかかっているのは8人(約7.5%)。検査で10人が陽性判定を受けたとすると、そのうち実際にヘルニアであるのはおおよそ1人未満ということですね。
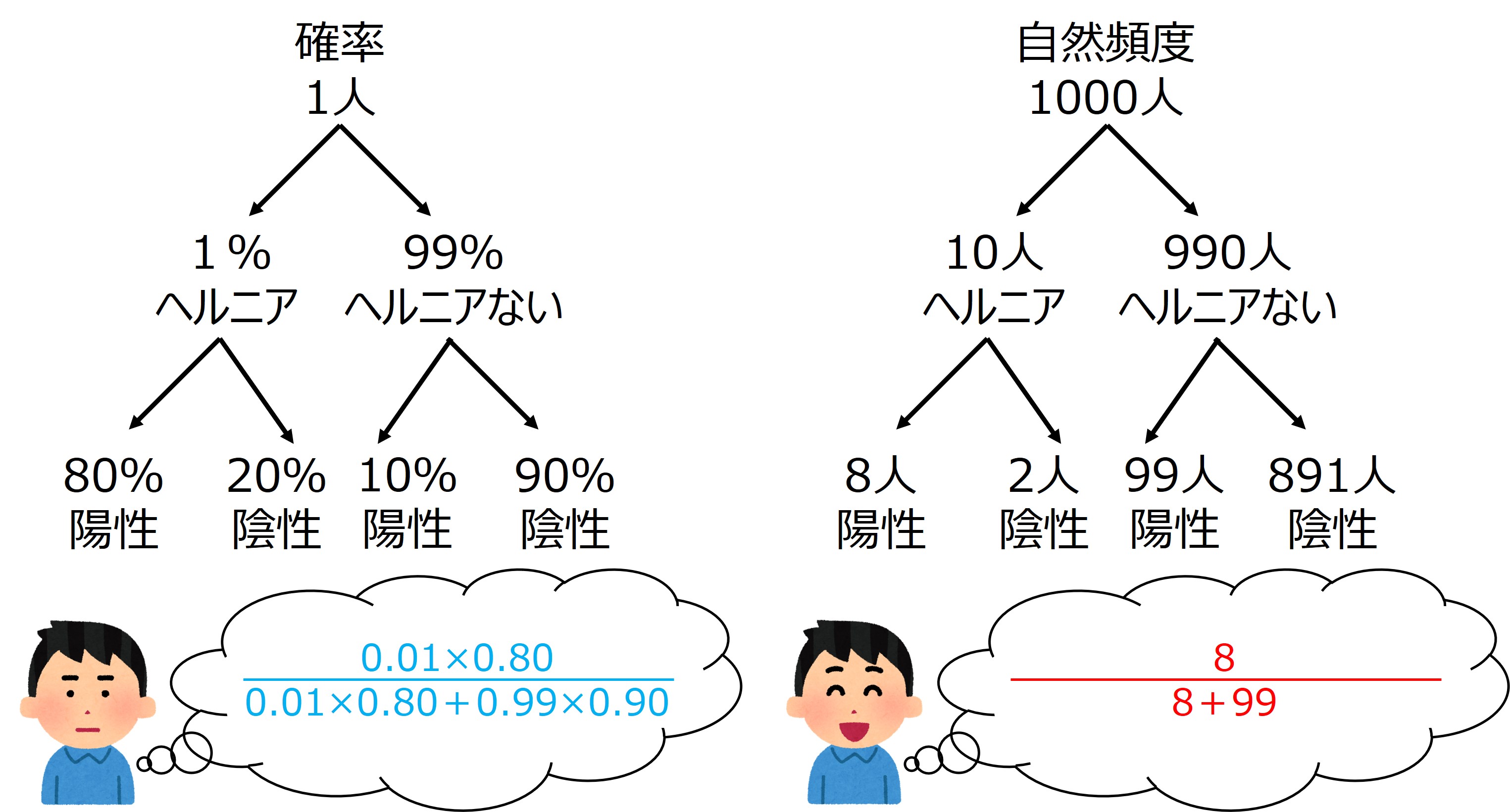
これらの数値(陽性的中率)は全体(母数)のなかの病気の多寡(多い少ない)で変わってきます。病気が多ければ陽性的中率は高くなりますし、少なければ低くなります。
こういった思考過程があると患者さんにリスクを伝えるときにもわかりやすく伝えることができますね。
◆自然頻度を使うための参考図書
以下の本が、リスクや自然頻度を理解するのに有用かと思われます。わたしとしては、読みやすさやなどから上の『賢く決めるリスク思考』をオススメしますが、『リスク・リテラシーが身につく統計的思考法』も安価で情報満載です。
また、リスク・リテラシーとともに幅ひろく健康似非科学を知りたい方は、『デタラメ健康科学』がオススメです。
①賢く決めるリスク思考
②リスク・リテラシーが身につく統計的思考法
③デタラメ健康科学
【資料】
(1)Statistical methods in the journal.[PMID:16267336]
(2)Medicine residents’ understanding of the biostatistics and results in the medical literature.[PMID:17785646]
(3)賢く決めるリスク思考、ゲルト・ギーゲレンツァー、インターシフト、2015
(4)ダメな統計学、アレックス・ラインハート、勁草書房、2017
[ad#ad3]